永乐大典·卷一万六千三百四十四算

卷一万六千三百四十四算

　　永乐大典卷之一万六千三百四十四　十翰

　　算〈算法十五〉

　　〈少广九章算经以御积羃方圆.淳风。按一畆之田。广一步。长二百四十步。今𣣔截取其从少。以益其广。故曰少广术曰。置全步。及分母子。以最下〉

　　〈分母。徧乘诸分子及全步淳风等。按以分母乘全者通其分也。以母乘子者。齐其子也。各以其母除其子置之于左命通分者又以分母徧乘诸分〉

　　〈子。及已通者。皆通而同之。并之为法。淳风等。按诸子悉通。故可并之为法。赤宜用合分术。列数尤多。若用乘则算数至繁。故别置此从省约。置所求〉

　　〈步数。以全步积分乘之为实。置所求步数。以全步积分乘之为实。此以田广为法。以畆积步为实。置有分者。当同其母。齐其子。以同乘法实。而并齐〉

　　〈于法。今以分母乘全步及子。子如母而一。并以并全法。则法实俱长意亦等也。故其法而一得从步数。实如法而一得从步。严恭通原箕法夏侯阳〉

　　〈经云。田土论文。积土论尺。评重论寸。平方一尺者。积一百寸。立方一尺者。积一千寸也。〉

　　〈九章算经今有田广一步半求田一畆。问从几何。答曰。一百六十步。〉

　　〈术曰。下有半。是二分之一。以一为二。半为一。并之得三为法。置田二百四十步亦以一为二乘之为实。实如法得从步。〉

　　〈今有田广一步半三分步之一。求田一畆。问从几何。答曰一百三十步。一十一分步之一十。〉

　　〈术曰下有三分以一为六半为三。三分之一为二。并之得一十一为法置田二百四十步亦以一为六乘之为实。实如法得从步。〉

　　〈今有田广一步半三分步之一四分步之一。求田一畆。问从几何。答曰一百一十五步五分步之一。〉

　　〈术曰下有四分以一为一十二半为六三分之一为四。四分之。一为三。并之得二十五以为法置田二百四十步。亦以一为一十二乘之为实。〉

　　〈实如法而一得从步今有田广一步半三分步之一四分步之一五分步之一。求田一畆。问从几何。〉

　　〈答曰一百五步一百三十七分步之一十五。术曰。下有五分以一为六十半为三十。三分之一为二十四分之一为〉

　　〈一十五。五分之一为一十二并之得一百三十七以为法。置田二百四十步。亦以一为六十乘之为实实如法得从步〉

　　〈今有田广一步半三分步之一四分步之一五分步之一。六分步之一。求田一畒问从几何〉

　　〈答曰九十七步四十九分步之四十七术曰下有六分以一为一百二十半为六十三分之一为四十。四分之〉

　　〈一为三十五分之一为二十四六分之一为二十.并之得二百九十四以为法。置田二百四十步亦一为一百二十乘之为实。实如法得从。〉

　　〈杨辉详解今有田一畆广一步半全步乃一分之一。半步是二分步之一。三分步之一。四分步之一五分步之一六分步之一问从数。〉

　　〈答曰。九十七步四十九分步之四十七解题此问田一畒为主以广求从但其中加分母分子。位次颇多。若用〉

　　〈合分互乘之法岂不繁剧古人弃合分之术。而以诸母自乘为全步之积分乘子。却以诸。母各除其子取其本积。并之为广而求问。特设少广〉

　　〈之问。法曰。列置全步。及分母子。而副置分母自乘。分母自乘。是求全步之积分也。以乘全步及子。各以本母除之。并之为法。齐子之意。以代互〉

　　〈乘。以全步积分乘畆步为实。法既通分。实亦合一体通分。实如法而一。为法除实也。少广。李淳风等曰。一畆之田。广一步。长二百四十步。今〉

　　〈截从少以益广故曰少广。古术曰。置全步。及分母子。以最下分母遍乘诸分子及全步淳风等。以分母乘全步者。通其分也。以母乘其子者。齐〉

　　〈其子也各以其母除其子。置之于左命通分者。又以母遍乘诸分子。及已通者皆通而同之并之为法淳风等诸子悉通。故可并之为法。亦以〉

　　〈宜用合分术列数尤多。若用乘则算数置繁。故别置此术从省约。置所求步数以全步积分乘之为实置所求步数以全步积分乘之为实。此〉

　　〈以田广为法一畆积步为实法有分者。当共其母。齐其子。以同乘法实。而并齐于法今以分母乘全步及子子如母而一并以并全法则实供〉

　　〈长意亦等也故如母而一实如法而一得从。按古草曰。本是三叚。古人文言之置全步及分母子一步二分之一三分之一。四分之一。五〉

　　〈分之一六分之一以最下分母六遍乘诸分子及全步六位各六。各以其母分母除其子置之于左全步得六二分之一得三三分之一得二。〉

　　〈四分之一得一余四分之二五分之一得一余五分之一六分之一得一命通分者用母除子则分子之内又有分子矣又以母遍乘诸分子。〉

　　〈已通者皆通而同之。母即分子之母。当以四分与五分遍乘诸子。内其全步。得一百二十其二分之一得六十其三分之一得四十。其四分之〉

　　〈一得三十其五分之一得二十四。其六分之一得二十。并之为法并得二百九十四。置所求步数二百四十。以全步积分一百二十乘之为实。〉

　　〈二万八千八百。此是第一呌。合云实如法而一。法有分者。当同其母。齐其子。欠诸分母三字。以同乘法实。而并齐于法。下文合云。实如法而〉

　　〈一。宜以田广一步。二分步之一。三分步之一。求田一畆四步。三分步之一。问从为题。即法有分者当同其母。齐其子之句。先以母二分。次以三〉

　　〈分。并乘全步及子三位各得六。以各母除子。并得十一。法云以同乘法实者。谓法实皆有分子。用诸母同乘其实。一畆四步。三分步之一。以分〉

　　〈母通为七百三十三。以分母六乘得四千三百九十八。仍以实母三同乘法得三十三。是并齐于法。下文便当云实如法而一。除得一百三十〉

　　〈三步。十一分步之三。以分母欠自乘而三字乘全步。及子。子如欠各母而一。欠并之为法。实如法而一得从。后草所编之术。草曰。列置全〉

　　〈步。及分母子。全步。即一分之一。以分母一。二。三。四。五。六。列右行。分子之一。一。一。一。一。一。列左行。而副置分母自乘。不动正位。别置分母自乘。得〉

　　〈七百二十。以乘全步及分子。全步得七百二十。分子皆为七百二十。各以本母除子。全步得七百二十。其二分之一得三百六十。其三分之一〉

　　〈得二百四十。其四分之一得一百八十。其五分之一得一百四十四。其六分之一得一百二十。并之得一千七百六十四。为法。以全步积分通〉

　　〈畆步。通二百四十步。为一十七万二千八百分。为实。实如法而一。以一千七百六十四分为法除实。得九十七步。余一千六百九十二。约之得〉

　　〈四十九分步之四十七九章算经今有田广一步半三分步之一。四分步之一。五分步之一。六分〉

　　〈步之一。七分步之一。求田一畆问从几何。答曰九十二步一百二十一分步之六十八。〉

　　〈术曰。下有七分以一为四百二十半为二百一十三分之一为一百四十。四分之一为一百五五分之一为八十四六分之一为七十七分之〉

　　〈一为六十并之得一千八十九以为法。置田二百四十步。亦以一为四百二十乘之为实。实如法得从步。〉

　　〈今有田广一步半三分步之一四分步之一。五分步之一六分步之一。七分步之一。八分步之一求田一畆问从几何。〉

　　〈答曰八十八步七百六十一分步之二百三十二术曰下有八分。以一为八百四十半为四百二十。三分之一为二百八〉

　　〈十。四分之一为二百一十。五分之一为一百六十。八六分之一为一百四十七分之一为一百二十八分之一为一百五。并之得二千二百八〉

　　〈十三以为法置田二百四十步亦以一为八百四十乘之为实。实如法得从步〉

　　〈今有田广一步半三分步之一。四分步之一五分步之一。六分步之一。七分步之一。八分步之一九分步之一求田一畆问从几何〉

　　〈答曰八十四步。七千一百二十九分步之五千九百六十四。术曰。下有九分。以一为二千五百二十。半为一千二百六十。三分之一〉

　　〈为八百四十。四分之一为六百三十。五分之一为五百四。六分之一为四百二十。七分之一为三百六十八分之一为三百一十五。九分之一〉

　　〈为二百八十。并之得七千一百二十九以为法。置田二百四十步。亦以一为二千五百二十乘之为实。实如法得从步。〉

　　〈今有田广一步半。三分步之一。四分步之一。五分步之一。六分步之一。七分步之一。八分步之一。九分步之一。十分步之一。求田一畆。问从几何。〉

　　〈答曰。八十一步。七千三百八十一分。步之六千九百三十九。术曰。下有一十分。以一为二千五百二十。半为一千二百六十。三分之〉

　　〈一为八百四十。四分之一为六百三十。五分之一为五百四。六分之一为四百二十七分之一为三百六十。八分之一为三百一十五。九分之〉

　　〈一为二百八十。十分之一为二百五十二。并之得七千三百入十一以为法。置田二百四十步。亦以一为二千五百二十乘之为实。实如法得〉

　　〈从步。今有田广一步半三分步之一。四分步之一。五分步之一。六分步之一。七〉

　　〈分步之一。八分步之一。九分步之一。十分步之一。十一分步之一。求田一畆。问从几何。〉

　　〈答曰。七十九步。八万三千七百一十一分。步之三万九千六百三十一。术曰。下有一十一分。以一为二万七千七百二十。半为一万三千八百〉

　　〈六十。三分之一为九千二百四十。四分之一为六千九百三十。五分之一为五千五百四十四六分之一为四千六百二十。七分之一为三千〉

　　〈九百六十。八分之一为三千四百六十五。九分之一为三千八十一。十分之一为二千七百七十二十一分之一为二千五百二十。并之得八〉

　　〈万三千七百一十一以为法置田二百四十步。亦以一为二万七千七百二十乘之为实。实如法得从步〉

　　〈今有田广一步半三分步之一。四分步之一。五分步之一。六分步之一。七分步之一。八分步之一九分步之一。十分步之一。十一分步之一。十二分〉

　　〈步之一求田一畆问从几何。答曰。七十七步。八万六千二十一分。步之二万九千一百八十三。〉

　　〈术曰。下有一十二分。以一为八万三千一百六十。半为四万一千五百八十三分之一为二万七千七百二十四分之一为二万七百九十。五〉

　　〈分之一为一万六千六百三十二。六分之一为一万三千入百六十。七分之一为一万一千八百八十。八分之一为一万三百九十五。九分之〉

　　〈一为九千二百四十一。十分之一为八千三百一十六。十一分之一为七千五百六十。十二分之一为六千九百三十。并之得二十五万八千〉

　　〈六十三以为法。置田二百四十步。亦以一为八万三千一百六十乘之为实实如法得从步。淳风等。按凡为术之意。约省为善。宜云下有一十〉

　　〈二分。以一为二万七千七百二十。半为一万三千八百六十。三分之一为九千二百四十。四分之一为六千九百三十。五分之一为五千五百〉

　　〈四十四。六分之一为四千六百二十。七分之一为三千九百六十。八分之一为三千四百六十五。九分之一为三千八十。十分之一为二千七〉

　　〈百七十二。十一分之一为二千五百二十。十二分之一为二千三百一十。并之得八万六千二十一以为法。置田二百四十步。亦以一为二万〉

　　〈七千七百二十乘之以为实。实如法得从步。其术亦得知不繁也。开方杨辉摘奇算法校正辩古通源。开方不尽之法。开方除不尽之数命〉

　　〈为分子术曰。倍隅数入廉一退。平方二因。立方三因。并入下法一算。緫为分母。以命分子之数。再求积数还源术曰。置方面全步。以分母通之。并〉

　　〈入分子。自乘于头。又以分子减分母余以分子乘之得数。并入头位为实。商除还原。无此一叚。以分母自乘为法。实如法而一平方本积有分子。〉

　　〈即是原方面有之分术曰。分母乘全步。并入分子。开方除得方面散分积数。别置原分母。开方除得方面分母。以除前叚散积乃得方面几步几分〉

　　〈之几杨辉详解开方作法本源。出释镇算书。贾宪用此术。〉

　　〔插图〕

　　〈左袤乃积右袤乃隅算。〉

　　〈中蔵者皆廉。以廉乘商方。〉

　　〈命实而除之。〉

　　〈增乘方求廉法草曰。释镇求廉本源。列所开方数。如前五乘方。列五位隅算在外。以隅算一。自下增入前位。至首位而止。首位得六。第二位得〉

　　〈五。第三位得四。第四位得三。下一位得二。复以隅算如前升增。逓低一位求之。〉

　　〈求第二位六旧数五加士而止四加六为士三加三为六二加一为三〉

　　〈求第三位六十五并旧数十加十而止六加四为十三加一为四〉

　　〈求第四位〉

　　〈六十五二十并旧数十加五而止四加一为五求第五位〉

　　〈六十五二十十五并旧五加一为六上㢘二㢘三㢘四㢘下㢘〉

　　〈杨辉纂类贾宪立成释鎻平方法曰。置积为实别置一算名曰下法。于实数之下自末位常超一位。约实至首位尽而止。实上商至第一位得〉

　　〈数下法之上。亦置上商。名曰方法命上商除实。二乘方法。一退为廉。下法再退于上商之次续商第二位得数扵廉法之次。照上商置隅。以方〉

　　〈廉二法皆命上商除实二乘隅法并入廉法一退。下法再退商置第三位得数下法之上照上商置隅以廉隅二法皆命上商除实尽。得平方〉

　　〈一面之数积有分子者以分母乘其全入内子又以分母再二次自乘乘之积圆者。以国法十二乘之。开平方求积。如分母自乘而一。增乘〉

　　〈开平方法曰。第一位上商得数以乘下法为平方命上商除实。上商得数以乘下法入平方一退为廉第二位再商得数。以乘下法为隅。命〉

　　〈上商除实讫以上商得数乘下法入隅皆名曰廉一退下法再退以求第三位商数第三位如第二位用法求之〉

　　〈贾通全能集开方以积使商除除得其间上置诸下另倍为方法数却将方倍减其余得其次数上商续方下旁邉也续欤上下再将续除积。积之〉

　　〈数尽自昭如若还不尽倍方次逐一将方位数除除见数来商又续。只将此续取空虚〉

　　〈开方之法有三有平方。有直方有立方其法最难取算。然公私亦少用之但平方一法间自用之收算。方田一面。不可不载一法于其间也。〉

　　〈丁巨算法方求圆。二十二乘七除圆求方。七乘二十二除。平面求周。圆十二乘方四乘外圆求积圆物六乘十二除。方物。八乘十六除。立圆求径。〉

　　〈九乘十六除立方求圆十六乘九除见斜求方。五乘。七除见方求斜。七乘。五除。〉

　　〈九章算经今有积五万五千二百二十五步。问为方几何答曰二百三十五步。〉

　　〈今有积二万五千二百八十一步。问为方几何。答曰。一百五十九步〉

　　〈今有积七万一千八百二十四步。问为方几何。答曰。二百六十八步。〉

　　〈杨辉详觧解题圜三象天。方四象地。圜居方四分之三。以积立术。求方助乘除之妙用。考究源流。莫不由此。法曰。置积为实。别置一算名曰下〉

　　〈法。原下之法。于实数之下。自末位常超一位。初乘时过一位。今超一位。约实至首位尽而止。一下定一。一百下定十。万下定百。百万下定千。于〉

　　〈实上商置第一位得数。以方法一一。二二。三三四四。五五。六六。七七。八八九九。之数为商。商本体实数。下法之上。亦置上商数。即原乘法数也〉

　　〈名曰方法。于本积内。去其一方。命上商除实。法实相呼。以破积数。二乘方法。一退为廉。一方带两直。以助其状如廉。故二乘退位。下法再退。下〉

　　〈法即定位之算。再退复位。于上商之次。续商第二位得数。与上意同。于廉。法之次。照上商置隅。一方带二廉。正阙一角。角即名隅。以方廉二法。〉

　　〈亦原乘之法也。皆命上商除实。二乘隅法并入廉法一退。倍隅人廉作一大方。以求次位得数。下法再退。前意商置第三位得数。下法之上。照〉

　　〈上商置隅。以廉隅二法。皆命上商除实。第二位解意同。得平方一面之数。更有不尽之数。依第三位体面倍隅入廉。退位商之。草曰。置积为〉

　　〈实。七万一千八百二十四步。别置一算为下法。原下之法。从末常超一位约实。百下约十。万下约百。实上商置第一位得数二百。下法之上。亦〉

　　〈置上商二百名曰方法二百乃命上商除实。四万余三万一千八百二十四。二乘方法得四百步一退为廉四百下法再退。百下约十。扵上商〉

　　〈之次续商第二位得数六十。共为二百六十。廉法之次。照上商置隅六十以廉隅二法皆命上商除实二万七千六百。余四千二百二十四。二〉

　　〈乘隅法并于廉。得五百二十。一退五百二十。下法再退。于末位下定一。又于上商置第三位得数二百六十之次。商置八。下法之上亦置八为〉

　　〈隅除实适尽合问〉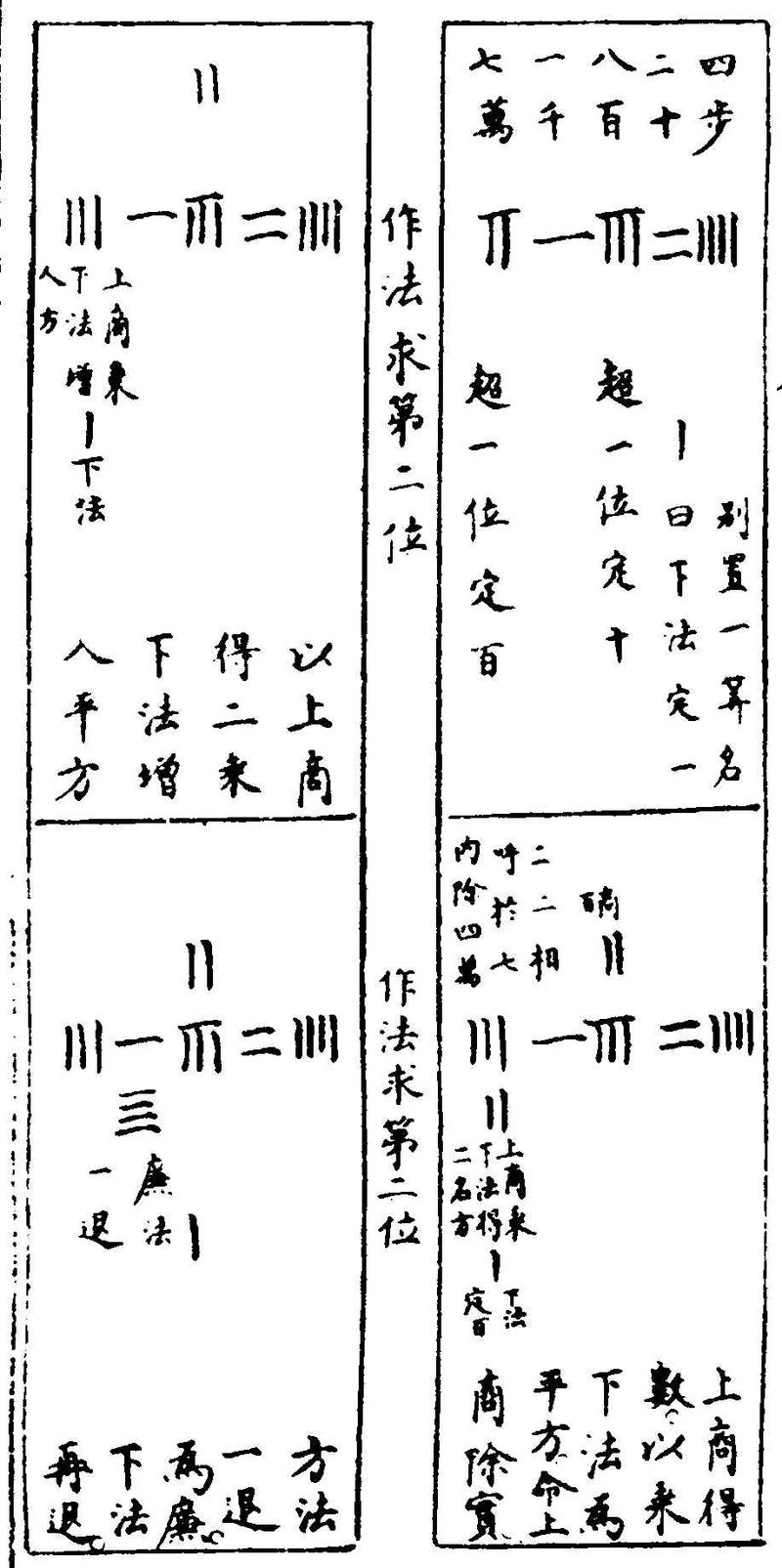

　　〔插图〕

　　〈增乘开平方法。以商数乘下法。逓增求之。商第一位。上商得数以乘下法为乘方。命上商除实。上商得数以乘下法入乘方。一退为廉。下法〉

　　〈再退。商第二位。商得数以乘下法为隅。命上商除实讫。以上商得数乘下法入隅皆名曰廉。一退。下法再退以求第三位商数。商第三位。〉

　　〈用法如第二位求之　增乘开平方图。以图参法。取用可知。〉

　　〈布位定位商第一位〉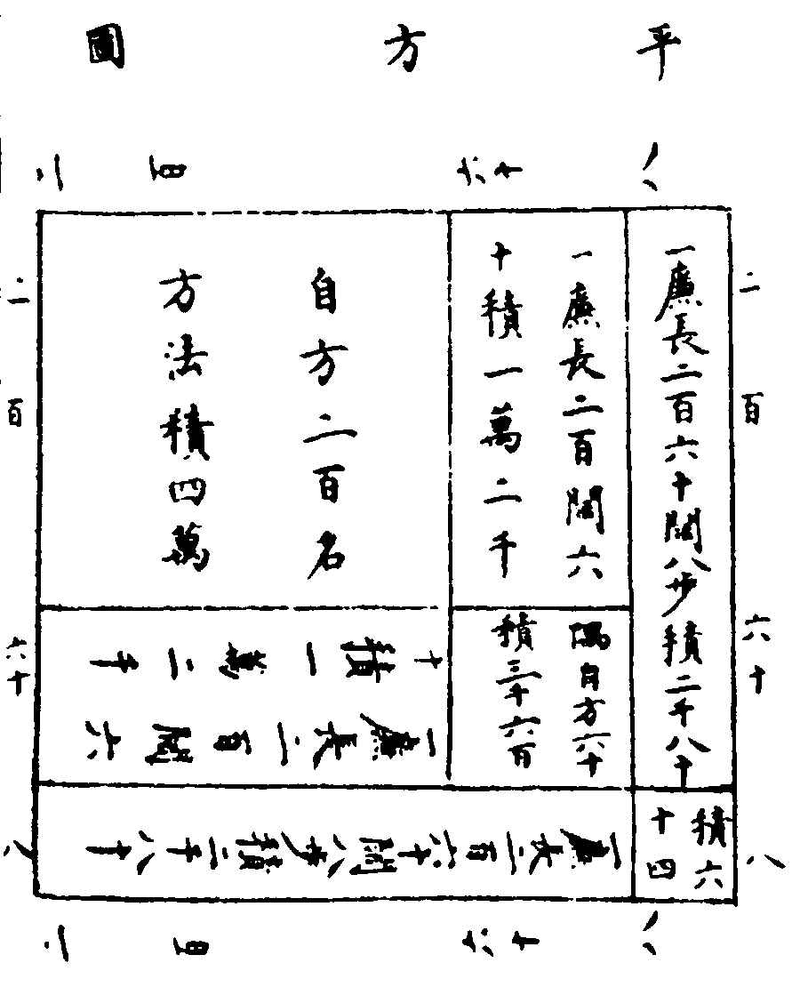

　　〔插图〕

　　〈商第二位作法求第三位〉

　　〔插图〕

　　〈严恭通原算法术曰。置积为实。借一算步之超一等。言百之面十也。言万之面百也。上商二百乘下隅为廉。二百呼除本积二二除去四万。余积〉

　　〈三万一千八百二十四步为实。倍廉为方法得四百。续上商六十乘下隅为廉六十。于四百之下与上商六十呼除本积。四六除去二万四千。〉

　　〈六六除去三千六百。余积四千二百二十四步为实。又倍廉六十得一百二十并入方法共五百二十。续上商八步乘下隅为廉八步。于五百〉

　　〈二十之下与上商八步呼除本积。五八除去四千。二八除去一百六十。八八除去六十四步适画。得方面二百六十八步合前问。〉

　　〈九章算经又有积五十六万四千七百五十二步。四分步之一。问为方几何。答曰。七百五十一步半。〉

　　〈严恭通原算法术曰。列积步以四分通之纳子。又以四分再自乘得六十四乘之为实。以开方法除之得一万二千二十四分。却以四分自乘〉

　　〈之。得一十六为法除之即得。今有积三十九亿七千二百一十五万六百二十五步。问为方几何〉

　　〈答曰。六万三千二十五步开方求方羃之一面也术曰置积为实借一算步之超一等。言百之面〉

　　〈十也。言万之面百也。议所得以一乘所借一算为法而以除。先得黄甲之面。上下相命是自乘而除也除已倍法为定法。倍之者豫张面面朱〉

　　〈羃定袤以待复除。故曰定法其复除折法而下欲除朱羃者本当副置所得乘方倍之为定法以折议乘而以除。如是当复步之而止乃得相〉

　　〈命故使就上折下复置借算步之如初以复议一乘之欲除朱羃之甫黄乙之羃。其意如初之所得也所得副以加定法以除以所得副从定〉

　　〈法。再以黄乙之面加定法者是则张两青羃之袤复除折下如前。若开之不尽者为不可开当以面命之术或有以借箕加定法而命分者。虽〉

　　〈粗相近不可用也。凡开积为方方之自乘当还复有积分令不加借算而命分则常微少其加借算而命分则又微多其数不可得而定故惟〉

　　〈以面命之为不失耳譬犹以三除十以其余为三分之一而复其数可以举。不以面命之加定法如前求其微数微数无名者以为分子。其一〉

　　〈退以十为母其再退以百为母退之弥十其分弥细。则朱羃虽有所乘之数不足言之也若实有分者通分内子为定实。乃开之讫开其母报〉

　　〈除。淳风等。按分母可开者并通之积先合二母。既开之后一母尚存。故开分母求一母为法以报除也。若母不可开者又以母再乘定实乃开〉

　　〈之讫。令如母而一。淳风等。按分母不可开者本一母也。又以母乘之乃合二母既开之后亦一母存焉。故令一母而一得全面也又按此术开〉

　　〈方者。求方羃之面也。借一算者假借一算空有列位之名而无除积之实。方隅得面。是故借算列之于下步之超一等者。方十自乘其积有百〉

　　〈方百自乘其积有万。故超位至百而言十。至万而言百。议所得以一乘所借算为法而以除者先得黄甲之面。以方为积者两相乘故开方除〉

　　〈之还令两面。上下相命是自乘而除之。除已倍法为定法者。实积未尽当复更除。故豫张两面朱羃袤以待复除。故曰定法。其复除折法而下〉

　　〈者欲除朱羃。本当副置所得成方倍之为定法。以折议乘之而以除如初。是当复步之而止乃得相命故使就上折之而下复置借算步之如〉

　　〈初以复议一乘之所得。副以加定法。以定法除者。欲除朱羃之角。黄乙之羃以所得副从定法者再以黄乙之羃加定法。是则张两青羃之袤。〉

　　〈故如前开之即合所问孙子算经今有积二十三万四千五百六十七步。问为方几何。〉

　　〈答曰四百八十四步。九百六十八分步之三百一十一术曰置积二十三万四千五百六十七步为实次借一算为下法。步之〉

　　〈超一位至百而止。商置四百于实之上副置四万。于实之下。下法之上名为方法命上商四百除实除讫。倍方法一退。下法再退。复置上商八〉

　　〈十以次前商副置八百于方法之下下法之上名为廉法。方廉各命上商八十以除讫倍廉法上从方法一退方法下法再退复置上商四以〉

　　〈次前副置四于方法之下。下法之上名曰隅法方廉隅各命上商四除实除讫上商得四百八十四。下法得九百六十八。不尽三百一十一。是〉

　　〈为方四百八十四步九百六十八分步之三百一十一。夏候阳算经今有田二十一顷七十八畆一百八十步。问为方几何。〉

　　〈答曰七百二十三步奇百七十一步。术曰先置顷畒扵上以二百四十步乘之得五十二万二千七百二十〉

　　〈步内零一百八十步以开方除之。借一算为下法步之超一位至百止。万上置上商七百。下亦置七万于实位之下。下法之上。命上商除实讫〉

　　〈倍方为一十四万。方法一退。下法再退。又置上商二十于前商后又置二百扵方法之下。下法之上。名曰隅法。以方隅二法皆命上商以除实〉

　　〈讫。倍隅法为四百从上。方法一退。下法再退。又置上商三于前商二十之后又置三步于方法之下。下法之上。名曰隅法。以方隅二法皆命上〉

　　〈商除实讫倍隅法得六从上。方法得一千四百四十六。即是上方得七百二十三步奇一百七十一步。〉

　　〈五经算术论语千乘之国法。子曰道千乘之国。注云。司马法六尺为步。步百为畆畆百为夫夫三为屋。屋三为井。井十为通。通十为成。成出革车〉

　　〈一乘然千乘之赋其地千乘也。今有千乘之国。其地千成。计积九十亿步问为方几何〉

　　〈答曰。三百一十六里六十八步。一十八万九千七百三十七。分步之六万二千五百七十六。〉

　　〈术曰。置积步为实。开方除之即得。按千乘之国。其地千成。方十里。置一城地十里。以三百步乘之得三千步。重张相乘得九百万步。又以千成〉

　　〈乘之得积九十亿步。以开方除之。即得方数也。开方法曰。借一算为下法。步之常超一位至万而止。置上商九万于实之上。又置九亿于实之下。〉

　　〈下法之上名曰方法。命上商九万以除实毕。倍方法九亿得十八亿乃折之方法一折。下法再折又置上商四千于上。以次前商之后。又置四〉

　　〈百万于方法之下下法之上名曰隅法。方隅皆命上商四千以除实毕。倍隅法得八百万上从方法得一亿八千八百万乃折之方法一折。下〉

　　〈法再折又置上商八百于上。以次前商之后又置八万于方法之下。下法之上名曰隅法。方隅皆命上商八百以除实毕。倍隅法得十六万上〉

　　〈从方法得一千八百九十六万乃折之方法一折。下法再折又置上商六十于上以次前商之后。又置六百于方法之下。下法之上名曰隅法〉

　　〈方隅皆命上商六十以除实毕。倍隅法得一千二百上从方法得一百八十九万七千二百乃折之。方法一折。下法再折又置上商八于上以〉

　　〈次前商之后又置八扵方法之下下法之上名曰隅法方隅皆命上商八以除实毕倍隅法得一十六上从方法下法一亦从之得一十八万〉

　　〈九千七百三十七分步之六万二千五百七十六以里法三百步除之得三百一十六里不尽六十八步即得方三百一十六里六十八步一〉

　　〈十八万九千七百三十七分步之六万二千五百七十六也杨辉摘奇算法积一千三百尺。问平方一面几尺。〉

　　〈答曰。三十六尺七十三分尺之四开方草曰。置积为实。一千三百。别置下法一算从常超一位约实。百下〉

　　〈定十。上商方面三十以乘下法为方法三十命上商除实九百。余实四百。以二因方法。一退为廉六十下法再退定零上又商第二位方面六〉

　　〈尺。以乘下法为隅六尺。以廉隅二法六十六尺命上商除实三百九十六尺余实四尺即开方不尽之数。二因隅法并入廉法。共七十二添入〉

　　〈下法一算共七十三。命为分母。所余四尺。命为分子合问还源求原积草曰。置方面三十六尺。七十三分尺之四。以分母通全尺并入分子〉

　　〈共二千六百三十二自乘于上。得六百九十二万七千四百二十四。别置分子减分母余分子四减分母七十三余六十九以乘分子。六十九〉

　　〈乘子四。得二百七十六。并之为实。得六百九十二万七千七百。以分母自乘为法。得五千三百二十九。以法除之。得原积一千三百尺。〉

　　〈今有积一千五百九十尺。六十四分尺之一。问平方面几何。答曰。三十九尺。八分尺之七。〉

　　〈原积有分子开平立术曰。以分母六十四。通积尺一千五百九十。分子一并之为实。一十万一千七百六十一。开平方得方面分子积数三百〉

　　〈一十九置原分母开方六十四。开平方得八。为方面分母。以除方面分积三百一十九。得方面尺数三十九尺。余八分尺之七。〉

　　〈透帘细草今有平方积五万五千六百九十六尺。问一面方多少。答曰。二百三十六尺。〉

　　〈法曰平立开之草曰。置积为实。借一算子为约法。常超一位。进二度合商百。乃上商二百尺。二因常隅。又名下法。又名约法。得二万为方法。〉

　　〈命商除实四万了。倍方法一退得四十。约法二退于百之下。续商三百尺。三因隅法得三百尺。并入立法得四千三百。命商三十除实。余有二〉

　　〈千七百九十六在方法内又添隅法三百一退得四百六十。隅法二退为二尺上续商六尺。又于方法内添隅法六尺一步。得四百六十六尺。〉

　　〈乃命商六尺除实恰尽丁巨算法术曰置积在地商二二如四除了四万另于上退二位置二合商百并于下置二为方倍之得四将四问得〉

　　〈四三一十二又除一万。二千于上续商三下方亦续三又将上下三为三三如九又除九百实有二千七百九十六又将立三倍为六共得四〉

　　〈六却以四商得四六二十四又除二千四百。续商六以六除尽。丁巨算法今有平方积六十二万二千五百二十一尺问一面几何。〉

　　〈答曰七百八十九尺置积尺以一算于一尺之下为隅常超一位至二万尺之下上商七呼〉

　　〈一七生方七。即扵隅法之上布七作方法。呼七七四十九去积四十九万尺。倍方法为一十四方法一退隅法二退上商八呼一八生方八。于〉

　　〈方法之后对上商八之下布方法八呼一八如八去积八万尺。余积五万二千五百二十一尺呼四八三十二去积三万二千尺又呼八八六〉

　　〈十四去积六千四百尺倍方法八得方法一百五十六。方法一退。隅法二退上商九呼一九生方九即于生法之后对上商九之。下布方法九〉

　　〈呼一九如九去积九千尺。呼五九四十五去积四千五百尺。呼六九五十四去积五百四十尺。九九八十一去积八十一尺适尽。此平方之法〉

　　〈颇难通。故复二例。若有积九千六百零四尺。开平方一面几何。然九十八尺。置积在地如上除也。〉

　　〈贾通全能集今有方田六畆零四步。问一方面该步几何。答曰。该方三十八步。〉

　　〈法曰。置畆为步。答入零步。开平方除之合问。开平本法。置緫法在地用商三三如九。另于上退二位置三合商十。下亦另置三为方法在地〉

　　〈止有五百四十四。却以方法三倍之得六。又以六商除六八四十八。续上商八在地。止有六十四方下亦置八。以八八呼除六十四恰尽。商得〉

　　〈三十八步为一方面。其余开方皆仿此。严恭通原算法今有积八万步问为方若干。〉

　　〈答曰二百八十二步。五百六十五分之四百七十六。术曰置积为实。借一算步之超一等上商二百乘下隅为廉。二百呼除〉

　　〈本积二二除去四万余积四万步为实。倍廉为方法得四百。续上商八十乘下隅为廉八十。于四百之下与上商八十呼除本积四八除去三〉

　　〈万二千。八八除去六千四百。余积一千六百步为实。又倍廉八十得一百六十。并入方法共五百六十续上商二步。乘下隅为廉二步。扵五百〉

　　〈六十之下与商二步呼除本积二五除去一千二六除去一百二十。二二除去四步。余积四百七十六步又倍廉二步得四并入方法并借一〉

　　〈隅算共得五百六十五是得方面二百八十二步五百六十五分之四百七十六合前问。〉

　　〈今有积一百二十一步问为方若干答曰。一十一步。〉

　　〈今有积三百六十一步。问为方若干。答曰。一十九步。〉

　　〈今有积七百步。问为方若干。答曰。二十六步。五十三分步之二十四。〉

　　〈今有积一千步。问为方若干。答曰。三十一步六十三分步之春十九。〉

　　〈术曰。俱以前开方除之即得。九章算经今有积一千五百一十八步。四分步之三。问为圆周几何。〉

　　〈答曰。一百三十五步。于徽术。当周一百三十八步。一十分步之一。淳风算。按此依宻平。为周一百三十八步。五十分步之九。〉

　　〈杨辉详解解题以方改圆验方圆相通也。圆居四分之三。法曰。分母乘全步入内。子以圆法十二乘之。又以分母再自乘乘之。开平方求积。以〉

　　〈分母自乘为法除之。以分母自乘为法除实得周。草曰。分母四。乘全步一千五百一十八步。入内子三。得六千七十五。以圆法十二乘之。得〉

　　〈七万二千九百。又以分母四。再自乘为六十四。乘之为实。四百六十六万五千六百。开平方别置一算为下法。原下之法。从末常超一位约实〉

　　〈百下约十。万下约百百万下约千。实上商置第一位得数二千。下法之上。亦置上商二千。名曰方法。乃命上商除实四百万。二乘方法一退为〉

　　〈廉。乘作四千退为四十。下法再退。百下定十。于上商之次续商第二位得数一百。共为二千一百。廉法之次。上商置隅一百。以廉隅二法皆命〉

　　〈上商除实。除四十一万。余二十五万五千六百。二乘隅法并为廉一退。得四千二百。下法再退。扵末位百下定十。又以上商置第三位得数六〉

　　〈十。下法之上亦置隅六十。除实适尽得二千一百六十。以分母自乘为法除之。严恭通原算法术曰。列积步。以四分通之纳子十二乘之。又以〉

　　〈四分再自乘得六十四。乘之为实。以开方除之。得二千一百六十分。却以四分自乘得一十六。为法除之即得。〉

　　〈今有积三百步问为圆周几何。答曰六十步于微术。当周六十一步。五十分步之十九淳风等。按〉

　　〈依宻率。为周六十一步一百分步之四十一。术曰。置积步数。以十二乘之。以开方除之即得周。此术以周三径一为〉

　　〈率。与旧圆田术相返覆也。于微术以三百一十四乘积。如二十五而一。所得开方除之即周也。开方除之即径是为据见羃以求周犹失之扵〉

　　〈微少。其以二百乘积一百五十七而一。开方除之即径。犹失之扵微多。淳风等。按此注于徽术求周之法。其中不用开方除之即径六字。今〉

　　〈本有者衍剩也。依宻率八十八乘之七而一。按周三径一之率。假今周六径二。半周半径相乘得羃三。周六自乘得三十六。俱以等数除羃得〉

　　〈一周之数十二也。其积本周自乘。合以一乘之。十二而一得积三也。术为一乘不长。故以十二而一得。此积。今还原。置此积三以十二乘之者〉

　　〈复其本周自乘之数。凡物自乘开方除之复其本数。故开方除之即周。孙子算经今有积三万五千步。问为圆几何。〉

　　〈答曰。六百四十八步。一千二百九十七分步之九十六。术曰。置积三万五千步。以一十二乘之得四十二万为实。次借一算为〉

　　〈下法。步之超一位至百而止。上商置六百。余于实之上副置六万。于实之下。下法之上。名为方法。命上商六百除实。除讫倍方法。方法一退。下〉

　　〈法再退复置上商四十。以次前商副置四百于方法之下。下法之上。名为廉法方廉各命上商以除实除讫。倍廉法从方法。方法一退。下法再〉

　　〈退。复置上商八次前商。副置八于方法之下下法之上名为隅法。方廉隅各命上商八以除实除讫倍隅法从方法。上商六百四十八。下法得〉

　　〈一千二百九十七不尽九十六是为方六百四十八步一千二百九十七分步之九十六〉

　　〈严恭通原算法今有积一千二百步欲为圆问径若干答曰四十步〉

　　〈术曰列积步以四乘三除得一千六百步以开方除之即得五径算术礼记投壶法。壶颈修七寸。腹修五寸。口径二寸半容斗五升注〉

　　〈云修长也。腹容斗五升三分益一则为二斗得圆囷之象积三百二十四寸。以腹修五寸约之所得求其圆周二尺七寸有奇是为腹径九寸有余〉

　　〈甄鸾按斛法一尺六寸二分上千之得一千六百二十寸为一斛积寸下退一等得一百六十二寸为一斗积寸倍之得三百二十四寸。为二斗〉

　　〈积寸以腹修五寸约之得六十四寸八分乃以十二乘之得积七百七十七寸六分。又以开方除之得圆周二十七寸余四十八寸六分倍二十七〉

　　〈从方法。得五十四。下法一亦从方法得五十五以三除二十七寸得九寸又以三除不尽四十八寸六分。得一十六寸二分与法俱上十之是为壶〉

　　〈腹径九寸。五百五十分寸之一百六十二母与子亦可俱半之为二百七十五分寸之八十一。淳风等。按其问宜云。今有壶腹修五寸容斗五升三〉

　　〈分益一则为二斗。得圆囷之象。问积寸之与周径各几何曰。积三百二十四寸。周二尺七寸。二百七十五分寸之二百四十三径九寸二百七十五〉

　　〈分寸之八十一。术宜云。置二斗以斗法乘之得积寸。以腹修五寸除之所得以十二乘之。开方除之得周数。三约之即得径数。〉

　　〈杨辉摘奇算法九章。立方积内原有分母开方术曰置全积通分并分子为实。开立方除得面积扵上。别置积内原分母如立方而一为法以〉

　　〈除。求出面积即得所答方面全步几分之几杨辉纂类贾宪立成释鎻立方法曰置积为实。别置一算名曰下法。于实数之下自末至首常超〉

　　〈二位。上商置第一位得数下法之上亦置上商又乘置平方命上商除实讫。取用第二位法。三因平方一退。亦三因从方面二退为廉。下法三〉

　　〈退。续商第二位得数。下法之上亦置上商为隅。以上商数乘廉隅。命上商除实讫。求第三位。即如求第二位取用。〉

　　〈九章算经今有积一百八十六万八百六十七尺。此尺。谓立方尺也。凡物有高深深而言积者曰立方问为立方几何。〉

　　〈答曰一百二十三尺。杨辉详解今问积中第一位是一立方自方百尺。第二位有三平方。各〉

　　〈方一百尺高二十尺其三廉各长一百尺。方二十尺。其一隅立方二十尺第三位积有三平方各方一百二十尺。高三尺。及三廉各长一百一〉

　　〈十尺。方三尺。其一隅立方三尺解题方自乘名为平方。又以方乘平方名曰立方状如骰子取用勾深致远之算。立方法曰。贾宪细草编为〉

　　〈活法置积为实别置一算名曰下法。原下之法于实数之下自末至首常超二位约实原乘之法过二位今还源故超二位一下定一。千下定〉

　　〈十百万下定百上商置第一位得数以方数为主。自乘求商。不𣣔迭注。详见细草下法之上亦置上商即平方面又乘为平方命上商除实讫。〉

　　〈除去一立方也三因平方一退亦三因从方面。二退为廉第一位得数乃立方其第二位有三个廉一小隅为助三因方廉退方一廉二者盖〉

　　〈其数有等第也下法三退原超二位今退三位。以定上商续商第二位得数下法之上亦置上商为隅第二位中隅见在解以上商数乘㢘隅〉

　　〈以平乘高命上商除实讫第二位取用如此求第三位即依第二位取用以上商乘廉三因隅法并入为方又以方法之下复置上商三因为〉

　　〈廉其方法一退㢘法再退下法三退续商第三位得数下法之上亦置上商为隅三因廉法隅自乘之皆命上商除实见第二位解适尽合问〉

　　〈草曰置积一百八十六万八百六十七尺为实。别置一算名曰下法于实数之下自末位常超二位约实。一下定一千下定十百万下定百〉

　　〈上商置第一位得数实数一百万上商置一百原定百也下法之上亦置上商一百乘为平方一百乘一百得一万尺乃命上商一百除实一〉

　　〈百万尺三因平方一退为三万尺。亦三因从方二退为廉三百尺下法三退定十续商置第二位得数二十下法之上亦置上商为隅二十以〉

　　〈上商乘廉得六千隅得四百。命上商除实讫。余一十三万二千八百六十七尺以上商二十乘廉得一万二千尺三因隅法得一千二百尺并〉

　　〈入方一退共四万三千三百尺。方法之下复置上商一百二十三因为廉三百六十廉法二退下法三退续商置第三位得数三尺下法之上〉

　　〈亦置上商为隅三尺。以上商乘廉一千八十。隅九尺。皆命上商除实适尽合问。增乘方法。立方原是乘而又乘至数。今以增乘为除求源草〉

　　〈曰。实上商置第一位得数一百。以上商乘下法置廉一百。乘廉为方一万除实讫复以上商一百乘下法入廉共二百乘廉入方共三万。又乘〉

　　〈下法入廉共三百其方一廉二。下三退定十再扵第一位商数之次复商第二位得数二十以乘下法入廉。共三百二十乘廉入方。共三万六〉

　　〈千四百命上商除实讫余一十三万二千八百六十七。复以次商二十乘下法入廉共三百四十乘㢘入方共四万三千二百尺。又乘下法入〉

　　〈廉共三百六十其方一廉二下三退如前。上商第三位得数三尺乘下法入廉共三百六十三乘廉入方共四万四千二百八十九。命上商三〉

　　〈尺除实适尽得立方一面之数。九章算经又有积一千九百五十三尺。八分尺之一问为立方几何。〉

　　〈答曰一十二尺半。今有积六万三千四百一尺五百一十二分尺之四百四十七。问为立方〉

　　〈几何答曰三十九尺八分尺之七。〉

　　〈杨辉详解解题此是带予立方。分母子立方法曰。置积以分母通其全。加内子为实。通分之意。开立方除之。前术得积。多分母子一叚。未可便〉

　　〈见方面。别置分母。如立方而一为法。母先曾乘而又乘。故如立方而一。除积还源。得立方一面之数。草曰。置积。以分母五百十二通全。六万〉

　　〈三千四百一尺。加内。子四百四十七为实。得三千二百四十六万一千七百五十九。开立方除之为积。得三百一十九。别置分母五百十二。如〉

　　〈开立方而一为法得八除积三百十九。得立方一面之数。前答。严恭通原算法术曰。置积以分母相乘纳子。三千二百四十六万一千七百五〉

　　〈十九分为积实。开立方除。借一算为下隅。常超二位约实。上商三百乘下隅得三百为廉法。以上商三百与廉三百乘得九万为方法。与上商〉

　　〈三百呼除本积三九除去二千七百万。余积实存五百四十六万一千七百五十九分为实。三因廉得九百。三因方得二十七万。续上商一十〉

　　〈乘下隅得一十。却乘廉九百得九千。并入方法。又以上商一十。乘下隅一十得一百。亦并入方法共二十七万九千一百分为方法。与上商一〉

　　〈十呼除本积一二除去二百万。再呼一七除去七十万。一九除去九万。一一除去一千。余积存二百六十七万七百五十九分为实。以扵方法〉

　　〈内更加原廉九千。又倍商乘隅得二百并入方法。次以上商三百一十三因得九百三十为廉法。续上商九分乘下隅得九分。却乘廉得八千〉

　　〈三百七十并入方法。又上商九分乘下隅九分。得八十一分亦并入方法。共二十九万六千七百五十一分为方法。与上商九分呼除本积二〉

　　〈九除去一百八十万。再呼九九。除去八十一万。六九除去五万四千。七九除去六千三百五九除去四百五十。一九除去九分适尽。得三百一〉

　　〈十九分为实。次置分母五百一十二。亦以开立方除之得八为法。实如法而一合前问。〉

　　〈今有积一百九十三万七千五百四十一尺。二十七分尺之一十七。问为立方几何。〉

　　〈答曰。一百二十四尺。太半尺开立方。立方适等求其一而也。术曰。置积为实借一算步之超二等。言〉

　　〈千之面十。言百万之面百。议所得以再乘所借一算为法而除之。再乘者。亦求为方幕以上议命而除之。则立方等也。除已。三之为定法。为当〉

　　〈复除。故豫张三面以定方羃为定法也。复除折而下复除者。三面方羃以皆自乘之数。须得折议定其厚薄尔。开平羃者。方百之面十。开立羃〉

　　〈者。方千之面十据定法也。有成方之羃故复除当以千为百。折下一等也。以三乘所得数。置中行设三廉之定长复借一算置下行。欲以为隅〉

　　〈方。立方等未有定数。且置一𥮅定其位步之中超一下超二位。上方法长自乘而析。中廉法但有长故降一等。下隅法无面长故又降一等也。〉

　　〈复置议以一乘中。为三廉备羃也。再乘下令隅自乘为方羃也。皆副以加定。法以定除。三面。三廉。一隅。皆已有羃。以上议命之。而除去三袤之〉

　　〈厚也。也除已。倍下并中从定法。凡再以中三以下加定法者三廉各当以两面之羃。连于三廉之端。以待复除也。言不尽意。解此要当以棊乃得〉

　　〈明耳。复除折下。如前开之。不尽者亦为不可开术亦有以定法命分者。不如故羃。开方以微数为分也。若积有分者。通分内。子为定实。定实乃〉

　　〈开之讫。开其母以报除。淳风等。按分母可开者并通之积。先合三母。既开之后。一母尚存。故开分母求一母为法。以报除也。若母不可开者。又〉

　　〈以母再乘定实。乃开之讫。令如母而一。淳风等。按分母不可开者。本一母也。又以母再乘之。今合三母。既开之后。一母犹存。故令一母而一得〉

　　〈全面也。按开立方。知立方适等求其一面之数。借一算步之超二位者。但立方求积。方再自乘。就积开之。故超二位。言千之面十。言百万之面〉

　　〈百。议所以再乘所借算为法而以除。知求为方羃以议命之而除。则立方等也。除已。三之定注为积。未尽当复更除。故豫张三面已定方羃为〉

　　〈定法复折除而下。知三面方羃。皆以有自乘之数。须得折议定其厚薄。据开平方百之面十。其开立方即千之面十。而定法已有成方之羃。故〉

　　〈复除之者当以千为百。折下一等。以三乘所得数置中行者设三廉之定长。复借一算置下行者。欲以为隅方。立方等未有数。且置一算定其〉

　　〈位也。步之中超一下二者。上方法长自乘而一折中。廉法但有长故降一等。下隅法无面长。故又降一等。复置议以一乘中者。为三廉借羃再〉

　　〈乘下当令隅自乘为方羃。皆副以加定法。以定法除者。三面。三廉。一隅。皆已有羃以上议命之而除去三袤之厚。除已倍下并中从定法者三〉

　　〈廉。各当以两面之羃连于两方之面一隅连于三廉之端以待复除其开之不尽者折下如前开方即合所问有分者通分纳子开之讫开其〉

　　〈母以报除可开者以通之积。先合三母。既开之复一母尚存。故开分母者求一母为法以报除若母不可开。者又以母再乘定实。乃开之讫。令〉

　　〈如母而一。分母不可开者本一母又以母再乘令合三母。既开之复亦一母尚存故令如母而一得全面。也。〉

　　〈透帘。细草今有立方积四千九百八十三万六千三十二尺。问立方一面多少〉

　　〈答曰三百六十八尺法曰开立方除之旧草冗繁今以透廉开之草曰列积为实。借一算〉

　　〈子名立隅又名约法常超二位约实两度进上合商三百。三因立隅得三百万别置为廉法又三因得九百万为方法只以方法命商除实二〉

　　〈千七百万三因方法为二千七百万一退三因廉得九百万二退。立隅法三退续商六十寸廉法内添隅添立隅六千共九万六千。六因加入〉

　　〈方法得三百二十七万六千命续商除实。余有三百一十八万三十二。在廉法内更添隅法六千得十万二千六因加入方法得三百八十八〉

　　〈万八千一退廉法内又添六千共十万八千二退。下法三退续商八寸。廉法内添隅法八寸共一千八十八乃八因加入方法得三十九万七〉

　　〈千五百四寸命商八寸除实恰尽严恭通原算法术曰。置本积为实。借一算为下隅常超二位约实上商二百尺乘下隅得三百尺为廉法。以〉

　　〈上商三百尺与廉三百尺相乘得九万尺为方法。与上商呼除本积三九除去二千七百万。余积上存二千二百八十三万六千三十二尺为〉

　　〈实。三因廉得九百尺。三因方得二十七万尺。续上商六十尺乘下隅得六十尺。却乘廉得五万四千尺并入方法。又上商六十尺与下隅六十〉

　　〈尺相乘得三千六百尺亦并入方法。共三十二万七千六百尺为方法。与上商六十尺。呼除本积三六除去一千八百万。再呼二六除去一百〉

　　〈二十万。再呼六七除去四十二万。再呼六六除去三万六千尺。余存三百一十八万三十二尺。再于方法内更加原廉五万四千尺。又倍商隅〉

　　〈三千六百得七千二百尺。亦并入方法共三十八万八千八百尺。次以上商三百六十三因得一千八十为廉法。续上商八尺乘下隅得八尺。〉

　　〈却乘廉得八千六百四十。又上商八尺与下隅八相乘得六十四尺。亦并入方法共三十九万七千五百四尺为方法。与上商八尺呼除本积〉

　　〈三八除去二百四十万。再呼八九除去七十二万。再呼七八除去五万六千。再呼五八除去四千尺再呼四八除去三十二尺适尽。得立方面〉

　　〈三百六十八尺合前问。丁巨算法今有积一万五千六百二十五尺。问为立方一面几何。〉

　　〈答二十五尺。置积尺。以一算于五尺之下常超二位。至位之下。上商二。呼一二生廉〉

　　〈二二二生方四。呼二四如八去积八千尺。余七千六百二十五尺。呼一二添廉二二四添方八又呼一二添廉二。方法一退。廉法二退。下法三〉

　　〈退上商五。呼五六生方三十五五生方二十五。命商除积。一五如五去积五十尺五五二十五去积二千五百尺。二五一十去积一百尺。五五〉

　　〈二十五去积二十五尺适尽。严恭通原算法今有积四万六千六百五十六尺。问立方面若干。〉

　　〈答曰。三十六尺。术曰。置本积为实。借一算为下隅常超二位约实。上商三十尺。乘下隅〉

　　〈得三十尺为廉法。以上商三十尺与廉三十尺相乘得九百尺为方法。与上商呼除本积。三九除去二万七千尺。余积实存一万九千六百五〉

　　〈十六尺为实。再以三因廉得九十尺。三因方得二千七百尺。续上商六尺乘下隅得六又却乘廉得五百四十尺并入方法。又上商六尺。与下〉

　　〈隅六尺相乘得三十六尺亦并入方法。共三千二百七十六尺为方法。与上商六尺呼除本积三六除去一万八千。再呼二六除去一千二百。〉

　　〈再呼六七除去四百二十。再呼六六除去三十六尺适尽。合前问。今有积七亿尺。问立方面若干。〉

　　〈答曰。八百八十七尺。二百三十六万二千九百六十九分尺之二百一十三万五千八百九十七。〉

　　〈术曰。置本积为实。借一算为下隅常超二位约实。上商八百尺。乘下隅得八百尺为廉法。以上商八百尺。与廉八百尺。相乘得六十四万尺为〉

　　〈方法。与上商呼除本积。六八除去四亿八千万。再呼四八除去三千二百万。余积实存一亿八千八百万尺为实。三因廉法得二千四百尺。三〉

　　〈因方得一百九十二万。续上商八十尺。乘下隅得八十尺。却乘廉得一十九万二千并入方法。又上商八十尺。与下隅八十尺。相乘得六千四〉

　　〈百尺亦并入方法。共二百一十一万八千四百尺为方法。与上商八十呼除本积。二八除去一亿六千万。再呼一八除去八百万。再呼一八除〉

　　〈去八十万再呼八八除去六十四万。再呼四八除去三万二千。余积实存一千八百五十二万八千尺为实。次于方法内更加原廉一十九万〉

　　〈二千又倍商乘隅得一万二千八百亦并入方法。共二百三十二万三千二百。次以上商八百八十三。因得二千六百四十为廉法。续上商七〉

　　〈尺乘下隅得七尺却乘廉得一万八千四百八十并入方法。又上商七尺。与下隅七尺。相乘得四十九尺亦并入方法。共二百三十四万一千〉

　　〈七百二十九尺为方法。与上商七尺呼除本积。二七除去一千四百万。三七除去二百一十万。四七除去二十八万。一七除去七千。七七除去〉

　　〈四千九百二七除去一百四十。七九除去六十三尺。余积存二百一十三万五千八百九十七尺。又于方法内更加原廉一万八千四百八十。〉

　　〈又倍商乘隅得九十八尺亦并入方法。次又以上商八百八十七尺。三因得二千六百六十一尺。更加原借一隅算亦并入方法。是得方面八〉

　　〈百八十七尺。二百三十六万二千九百六十九分尺之二百一十三万五千八百九十七。合前问。〉

　　〈今有积七亿二千一百七十三万四千二百七十三尺。问立方面若干。答曰。八百九十七尺。〉

　　〈今有积七十亿尺。问立方若干。答曰。一千九百一十二尺。一千九十七万二千九百六十九分尺之〉

　　〈一千二十一万七千四百七十二。今有积八十亿尺。问立方面若干。〉

　　〈答曰。二千尺。术曰。俱以前开立方除之即得。〉

　　〈杨辉纂类开立圆者。先以方法十六乘积。如圆法九而一开立方除之。积有分母子者通。母内子立圆用十六乘九除。开立方除之得积。别置分母〉

　　〈如立方而一。为法除积求之。增乘方法曰。实上商置第一位得数。以上商乘下法置廉。乘廉为方除实讫。复以上商乘下法入廉。乘廉入方。又乘下〉

　　〈法入廉其方一廉二。下三退。再扵第一位商数之次。复商第二位得数以秉下法入廉乘廉入方命上商除实讫。复以次商乘下法入廉。乘廉入方〉

　　〈又乘下法入廉其方一廉二。下三退。如前。上商第三位得数。乘下法入廉乘廉入方命上商除实适尽得立方一面之数。〉

　　〈九章算经今有积四千五百尺。亦谓立方之尺也。问为立圆径几何。答曰二十尺依宻率立圆径二十尺。计积四千一百九十尺。二十一〉

　　〈分尺之一十今有积一万六千四百四十八亿六千六百四十三万七千五百尺。问为〉

　　〈立圆径几何。答曰一万四千三百尺依宻率为径一万四千六百四十三尺。四分〉

　　〈尺之三术曰置积尺数以十六乘之九而一所得开立方除之即九径。立圆即〉

　　〈九也。为术者盖依周三径一之率令圆羃居方羃四分之三圆囷居立方亦四分。之三更令圆囷为方率十二为丸率九丸居圆囷又四分之〉

　　〈三也置四分自乘得十六三分自乘得九。故丸居立方十六分之九也。故以十六乘积九而一。得立方之积。丸径与立方等。故开立方而除得〉

　　〈径也。然此意非也。何以验之取立方綦八枚。皆令立方一寸。积之为立方二寸。规之为圆囷径二寸。高二寸。又复横因之则其形有似牟合方〉

　　〈盖矣。八棊皆然。似阳马圆然也按合盖者。方率也。丸居其中即圆率也推此言之。谓夫圆囷为方率岂不阙哉。以周三径一为圆率。则圆羃伤〉

　　〈少。令圆困为方率。则丸积伤多。互相通补。是以丸与十六之率。隅与实相近而丸犹伤多耳。观立方之内。合盖之外。虽衰杀有渐。而多少不掩。〉

　　〈判合緫结。方圆相缠。浓纤诡互。不可等正。欲陋形措意。惧失正理。敢不阙疑以俟能言者。黄金方寸重十六两。金丸径寸重九两。率生于此。〉

　　〈未曾验也周官考工记𣓨氏为董叚煎金锡则不耗不耗然后权之。权之然后凖之凖之然后量之言炼金使极精而后分之。则可以为率也〉

　　〈今丸径自乘三而一开方除之。即丸中之立方也。假令丸中立方五尺。五尺为勾勾自乘羃二十五尺倍之得五十尺。以为股羃。谓卑面方五〉

　　〈尺之弦也。以此弦羃为股。亦以五尺为勾。并勾股羃得七十五尺。是为大弦羃。开方除之。则大弦可知也。大弦则中立方之长邪。邪即九径。故〉

　　〈中立方自乘之羃。于九径自乘之羃三分之一也。今大弦还乘其羃。即丸外立方之积也。大弦羃开之不尽。令开羃七十五。再自乘之为面。命〉

　　〈得外立方积四十二万一千八百七十五尺之面。又令中立方五尺自乘。又以方乘之。得积一百二十五尺。一百二十五尺自乘为面。勾得积〉

　　〈一万五千六百二十五尺之面。皆以六百二十五约之。外立方积六百七十五尺之面。中立方积二十五尺之面也。张衡算。又谓立方为质。〉

　　〈立圆为浑。衡言质之与中外之浑六百七十五尺之面。开方除之不足一。谓外质积二十六也内浑二十五之面。谓积五尺也。今微令质言中〉

　　〈浑。浑又言质则。质相与之率。犹衡二浑相与之率也。衡盖亦先二质之率。推以言浑之率也。衡又言质六十四之面浑二十五之面。质复言〉

　　〈浑。谓居质八分之五也又云方八之面圆。圆浑相推知其复以圆囷为方率。浑为圆率也失之远矣衡说之自然欲恊其阴阳奇偶之说而不〉

　　〈顾疏宻矣。虽有文辞。斯乱道破义病也。置外质积二十六。以九乘之。十六而一。得积十四尺八分之五即质中之浑也。以分母乘全内子。得一〉

　　〈百一十七。又置内质积五。以分母乘之得四十。是谓质居浑一百一十七分之四十。而浑率犹为伤多也。征令方二尺。方四面并得八尺也。谓〉

　　〈之方周其中今圆径与方等亦二尺也。丸半径以乘圆周之半即圆羃也。半方以乘方同之半即方羃也。然则方周如方羃之率也。圆周知圆〉

　　〈羃之车也。按如衡术。方周率八之面。圆周率五之面也。今方周六十四尺之面。即圆周四十尺之面也。又令径二尺自乘得径四尺之面。是为〉

　　〈圆周率十二之面。而径率一之面也。衡亦以周三径一之率为非。是故更着此法。然增周太多过其实矣。淳风等。按祖暅之谓刘徽。张衡。二〉

　　〈人皆以圆囷为方率。丸为圆率。乃设新法。祖暅之间立圆术曰。以二乘积。开立方除之即立圆径。其意何也。取立方棊一枚。令立枢扵左后之〉

　　〈下隅。从规去其右上之廉。又合而横规之。去其前上之廉。于是立方之棋分而为四规。内棋一谓之内棊规。外棊三谓之外棊规。更合四棊后〉

　　〈横断之。以勾股言之。令余高为勾。内棊断上方为股本方之数其弦。勾股之法以勾羃减弦羃。则余为股羃。若令余高自乘减本方之羃。余即〉

　　〈内减其断上方之羃也。本方之羃。即外四棊之断上羃。然则余高自乘即外三棊之断上羃矣。不问高卑势加然也。然固有所归同而途殊者〉

　　〈尔。而乃控远以演类。借况以析𢕄。按阳马方高数参等者列而立之。横截去上则高自乘。与断上羃数亦等焉。夫迭棊成立积。缘羃势既同。则〉

　　〈积不客异。由此观之。规之外三棊旁蹙为一。即一阳马也。三分立方。则阳马居一。内棊居二可知矣。合八小方成一大方。合八内棊成一合盖。〉

　　〈内棊居小方三分之二。则合盖居立方亦三分之二。较然验矣。置三分之二。以圆羃率三乘之。如方羃率四而一。约而定之以为九率。故曰九〉

　　〈居立方三分之一也。等数既宻。心亦昭晰。张衡放旧。贻哂于后。刘徽循故。未暇校新。夫岂难哉。抑未之思也。依率立此圆积。本以圆径再自乘。〉

　　〈十一乘之。二十一而一约此积。今欲求其本积。故二十一乘之。十一而一。凡物再自乘开立方除之。复其本数。故立方除之即九径也。〉

　　〈杨辉详解积一百六十四万四千八百六十六尺四寸三分七厘五毫。问为立圆径几何。〉

　　〈答。一百四十三尺。解题立圆其状如球。居立方十六分之九。立圆法曰。以方法十六乘积。〉

　　〈如圆法九而一为实。平圆居平方四分之三。更添一乘为立圆立方。其立圆居立方十六分之九。取以为法十六乘。九而一。即互换之意。开增〉

　　〈乘立方除之前注草曰。置积题数以方法十六乘之。以九除之为实。得二百九十二万四千二百七尺开增乘立方除之。立草在九章卷〉

　　〈首布置圆内透帘细草今有立方圆积九百二十七寸。问径多少。〉

　　〈答曰一尺二寸法曰。置积寸以十六乘之九而一得一千七百二十八寸为实。开立方〉

　　〈除之即得。合问草曰十六乘之九除者。添入角积也。改立圆为立方是以开立方见一面数。。丨隅法三进在千之下。置廉一千。方一〉

　　〈千。除实一千方三因一为三千一退廉三因得三千二退。下位三退。续商二寸廉法内添隅法二寸得三十二寸。二因添入隅法得三百六十〉

　　〈四。命商除实尽也今有立方。圆平方各一所共计积二十二万九千六百七尺。只云立方面〉

　　〈多如立圆径七尺其平方面如立圆径三分之二。问三事各多少。答曰。立方面五十五尺。立圆径四十八尺。平方面三十二尺。〉

　　〈法曰。以立方开之。草曰。置共积二十二万九千六百七尺在地。于头位以多七尺自乘得数。又以七尺再乘之得三百四十三尺减扵头位〉

　　〈共积余有二十二万九千二百六十四。又以一百四十四为分母乘之。头位共得三千三百一万四千一十六尺为实置于头位。又多数七尺〉

　　〈自乘得数以四百三十二乘之得二万一千一百六十八尺为从法。又多七尺乘四百三十二得三千二十四。又添入六十四共得三千八十〉

　　〈八为廉常。以二百二十五为隅。立方开之。计积为实三千三百一万四千一十六于头位。从法二万一千一百六十八扵下位廉法三千八十〉

　　〈八于从法下。隅法二百二十五于廉之下。从法一进。廉法二进。隅法三进上商四共隅法相呼四因廉法得一百二十万八千八百。廉法相呼〉

　　〈生于从法得五百四万六千八百八十。命商除之。余有一千二百八十二万六千四百九十六。又四因隅法生于廉法得二百一十万八千八〉

　　〈百。又生于从法得一千三百四十八万二千八十。又四因扵廉法得三百万八千八百又八因隅法一退于廉得三百一十八万八千八百。从〉

　　〈法一退廉法二退隅法三退上商八生于廉法得三万一千八百八十八又八生扵从法得一百六十万三千三百一十二命商除之恰尽。得〉

　　〈立圆径内加七尺为立方面二因三除为平方面也合问今有圆球一。只径一尺二寸问计积寸多少〉

　　〈答曰。九百七十二寸。法曰。径再自相乘得一千七百二十八寸。又以九之。如十六而一。得积〉

　　〈寸合问。草曰径再自相乘为立方比立圆球子多四角积寸。一十六分之九。立圆积是十六分之九。先九因而后十六除者。恐有不尽免通分也。〉

　　〈严恭通原算法今有积二十六万六千九百三十五尺半。欲为立圆。问径若干。答曰。七十八尺。〉

　　〈术曰。置本积以十六乘之。得四百二十七万九百六十八尺。九除之得四十七万四千五百五十二尺为实。以开立方除。借一算为下隅。常超〉

　　〈二位约实。上商七十尺乘下隅得七十尺为廉法。以七十尺与上商七十尺相乘得四千九百尺为方法。与上商七十尺呼除本积。四七除去〉

　　〈二十八万七九除去六万三千。余积实存一十三万一千五百五十二尺为实三因廉得二百一十尺。三因方得一万四千七百尺。续上商八〉

　　〈尺乘下隅得八尺。却乘廉得一千六百八十尺并入方法。以上商八尺乘下隅得六十四尺亦并入方法。共一万六千四百四十四尺为方法。〉

　　〈与上商八尺呼除本积。一八除去八万。六八除去四万八千。四八除去三千二百四八除去三百二十。四八除去三十二适尽。得圆径七十八〉

　　〈尺合前问。今有积七百三十五万七千五百尺。欲为立圆。问周若干。〉

　　〈答曰。七百六尺。一百四十九万七千四百二十七分。尺之一百二十六万四千一百八十四。〉

　　〈术曰置积以一百四十四乘得一十亿五千九百四十八万。又三除之。得三亿五千三百一十六万尺为实。以前开立方除之即得。〉

　　〈杨辉详解积一百三十三万六千三百三十六尺。问为三乘方几何。答曰。三十四尺。〉

　　〈解题三度相乘。其状匾直逓增三乘开方法草曰。上商得数下法增为立方除实即原乘意。置积为实。别置一算名曰下法。扵实末常超三位〉

　　〈约实一乘超一位三乘超三位。万下定实上商得数三十。乘下法生下廉三十乘下廉生上廉九百乘上廉生立方二万七千。命上商除实。余〉

　　〈五十二万六千三百三十六。作法商第二位得数。以上商乘下法入下廉共六十。乘下廉入上廉共二千七百。乘上廉入方共一十万八千。又〉

　　〈乘下法入下廉共九十乘下廉入上廉共五千四百。又乘下法入下廉共一百二十方一上廉二下廉三下法四退。方一十万八千。上廉五千〉

　　〈四百下廉一百二十。下法定一又于上商之次续商置得数第二位四。以乘下法入廉一百二十四乘下廉入上廉共五千八百九十六。乘上〉

　　〈廉并为立方一十三万一千五百八十四命上商除实尽。得三乘方一面之数如三位立方。依第二位取用又术曰两度开平方开第一次〉

　　〈平方得一千一百五十六。开第二次平方得三十四。〉

　　永乐大典卷之一六千三百四十四

虚阁网(Xuges.com)