| 虚阁网 > 类书 > 图书集成乾象典 | 上页 下页 |
| 日月部汇考二 |
|
|
|
▼明,汤若望《新法历引》 《交食》 凡日月之行二十九日有奇,而东西同度,谓之“会朔。”至若日行在黄道近交,人视为与日同经同纬,是人目与日月相参直,而月魄正隔日光,于人目则为日食。日食者,非日失其光,光为月掩耳。凡太阴距太阳百八十度,而正与之冲,谓之望。若当冲时,月行近于两交,必入地景而为暗虚。此乃日月同在一线,而地居其中间,日光为地所阻,不能射照月体,则月失其光而为月食。此日月二食者,躔度有恒,持筹推步,分秒确然,而历家各法之疏密,于此更难掩也。试言其略,黄白二道相交之二所,名“正交、中交。”凡日月行及二交为同度,同度则有食矣。然而论交又须论限,及交而在限内则食,限外则不食,此不可不审也。顾限度诸方不一,盖太阳于诸方之地,平高度不同,而阴阳二历之各限亦异。论暖带下之地,二历互相受变。 如白道向南极半周,有时在天顶及黄道之中,势必反谓为阴历;白道向北半周,是时在黄道外,势必反谓为阳历。故其下日食之限,莫得而定之也。他域更近于北,必阴历限多,阳历限少;更近于南,必阳历限多、阴历限少。比如京师近北,约算阳历八度、阴历二十一度,则知日月相会。凡在阳历近二交八度,在阴历近二交二十一度,其下必见日食。而过此限以往,则否,即北可以推南,莫不以远近分多寡矣。然而二历食限之度有异者,其故盖在月轮。月轮比日最近于地,而月又小于地。人目见月之所又在地面,不在地心,故以月天论地平。虽天与地球皆为平分,直过其心,而人在地面高,所以视天地之两界,则似地球与月天,非平分也。少半在上,多半在下,而差约一度。 故以本法推算,月已出正地平,其于人目所视之地平,尚少一度。此其较谓之“视差。”盖惟月在天顶正地平与视地平之极,皆以一直线合于天顶,无有视差。 过此左右,不免有差。愈远天顶愈近,地平差必愈甚。 夫视差无他,恒降下月体数十分耳。设令日月同度,同在近交之南,又因同度并在正地平上高二十度,则太阳于视地平为十九度五十八分,祇降二分,太阴于视地平为十九度,直降一度矣,而日月二差之较为五十八分。故以算论,虽二曜同高同度,而人目视之,太阴恒下于太阳,一度弱,不掩日光则不食。若二曜在地平上高七十度,则太阳无视差。太阴视差止二十分,其降于太阳亦止二十分,势必相切,或至掩数分而成食。若二曜在交北,又当以太阴算在太阳之上,庶因视差所降,而掩阳光以为食也。顾此二地平之差,又分二类:一加减交食分数,谓之气差;一加减时刻,谓之时差。历算之艰且剧,莫过于此,所最当究心者也。 日食之全与不全,其故有二:一由天上之行,一由食时地平上高弧之度,故均一食也。有见全食者,有见食多寡不等者,有全不见食者。就南北论,见食地界,设如北京见全食,其南北各距四十五度之地,为万一千有余里,皆见有食,然而多寡不等。就东西论,各距六十度为万五千有余里,各见食而分数多寡亦不等焉。即月食时刻,南北亦有不同,而东西为甚也。 ▼《浑天仪说》 《太阳及太阴本行合宗动之验》 太阳为时日之原。一日约东行一度,于黄道为正,而于赤道恒为斜。或在两道之交,或北上,或南下,绝无定居,故无一定之时。此四季所繇以变易也。迨加以宗动,即见其出没之广不一,昼夜之长短有变。如日在降娄初度为春分,则出正东,没正西,昼与夜皆等。 自此以往渐斜去赤道北,出没较前为广矣。昼长而夜短,至夏至为最矣。乃从夏至而退行一度,其出其没,其昼其夜,与前所得等,渐退行,渐与前等。惟过秋分而太阳行赤道南,则于前后相对,宫度有定比例,彼之所广,此之所狭,彼之所长,此之所短,若相背而驰者然。 太阴依本行随黄道,约二十九日有奇,而与太阳会,故并论《宗动》则出没之广,在地平上下之时,皆从赤道纬,仿太阳为则,且无本光借光于日,因体厚不能透所借之光,故依本行距日远近不等,有时显全光,有时少显其光,只至正相望而食于地,景正相会,而能自以其体掩日原光。又依《宗动》使下地视之,时有先后,方位各异。兹有《本论》,聊述一二如此。 《求日月食之原》 日月地三体,必并居一直在线,始有食。盖日体恒居一直线之初界,而彼界则月体、地体迭居焉。如月体居界末,则月面之日光食于地景;地体居界末,则地上之日光食于月景。〈月体厚不能透光故〉“但太阳本行恒依黄道中线,而地居天之中心,一为日光所照,则此面受光,彼面必生景,虽所射景与日正对,亦不能越黄道之中线以为规也。乃太阴本行多在黄道内外,大端距日与地所居之直线远,则朔望无食。”惟出入黄道之处,与日与地相参直在一在线,则朔望必食。试于本仪考之,设太阴在阴。〈黄道北〉《阳历》:〈黄道南〉距两交甚远,任太阳在何宫度,使转太阴本圈与日体会为朔或正对为望。从而视之,必日月不能与地并居一直线,无缘得食。若移太阴至正交或中交,不拘得何宫度,与日相会或相望,必日月地之体并居一直线,本朔望时虽欲不食,不可得也。 ▼《测食》 《似食实食说》 人恒言日食月食矣,辄概混焉。不知月实食日,则似食而实非食也。何者?日为诸光之宗,永无亏损,月星皆借光焉。朔则月与日为一线,月正会于在线,而在地与日之间。月本厚体,厚体能隔日光于下,于是日若无光,而光实未尝失也,恶得而谓之食?望则日月相对,而日光正照之,月体正受之,人目正视之,月光满矣。此时若日月正相对如一线,而地体适当在线,则在日与月之间,而地亦厚体厚体隔日光于此面,而射影于彼面,月在影中,实失其所借之光,是为食也。然其食,特地与月之失日光耳。而其光之失,因光在地面与月体之上,地与月互相遮掩耳,日固自若也。总之,日也、月也、地也,使三体并不居一直线,则更无食矣。若食,则日体恒居一直线之界末,而彼界则月体地体迭居焉。月体居界末,则月面之日光食于地影矣。地体居界末,则地之日光食于月影矣。 《日食月食辩》 夫日食与月食,固自有异。盖月食天下皆同,而日食则否。日食,此地速,彼地迟,此地见多,彼地见少;此地见偏南,彼地见偏北,无有相同者也。而月食则凡地面见之者,大小同焉,迟速同焉,经候同焉,唯所居不同子午线者,则时刻不同矣。盖月一入影,失其借光,更无处可见其光也。 《因食而知日月地大小之别》 问:“日体甚大于月,与地何征?”曰:“昔有人叹世人止凭肉目,不求物理。尝设喻曰:‘日出地时,设有骏马疾驰,从日始露至全现,亦可驰四里。纵令日行与马等速则四里,而仅见其全,则全体之径亦必四里矣。今骏马一昼夜所驰,于地几何?最速不过全围百分之一也。而太阳日一周焉,则其行之疾莫拟也。是则马之’”四里,日之行几千万里矣。日体之大,即此微可知也。 且日月体之大小,即食可辨。盖凡物之有形象者,若空中无所障碍,则其体之全体之分,无不出其本象于一直线而至乎界之一点。此凡物皆然,不拘方圆棱角等形,如有物体于此,其基址即物体也,其界点则线之锐角所至,而入人目者也。凡“实体出《锐角》影者,照体必大乎实体,否则其光不能照实体之全面,而使对面锐影之尽处,仍聚合而有光也。”今欲验日大乎月,可视日食。月居日前而掩其光,是时月边尚有光,是日体在外。而其象之入人目,非近来自月体,乃远来自日体也。其线既为角形,则从月体至日体更为广大,是其角形之锐,从日来目为一点,而中间能包月体有余,则日体之大于月体,复奚疑哉? 今欲知日体大乎地者,观诸月食可知月之食地,居日前而生角,影掩月体也。当月食时,月体近乎地则入阔,影远乎地则人锐,影愈远愈锐,以聚于一点。若此者孰不信日体之大于地体也?设谓日体与地体均,则地影“大小均,为无穷尽之等影。”若言地体大乎日体,则地影必益远益大,为无穷尽之大影。其影既远,不独食诸天之星,必且食诸星之天矣。则每遇望时,月体讵能移于大影之外乎?由此益信月体之小乎地球也。盖地影益远益锐,而月食居此。影或有全而久者,则月径更小于影,而影小于地。故月体地球之大小从可知矣。 ▼《历象图说》 日月合朔图 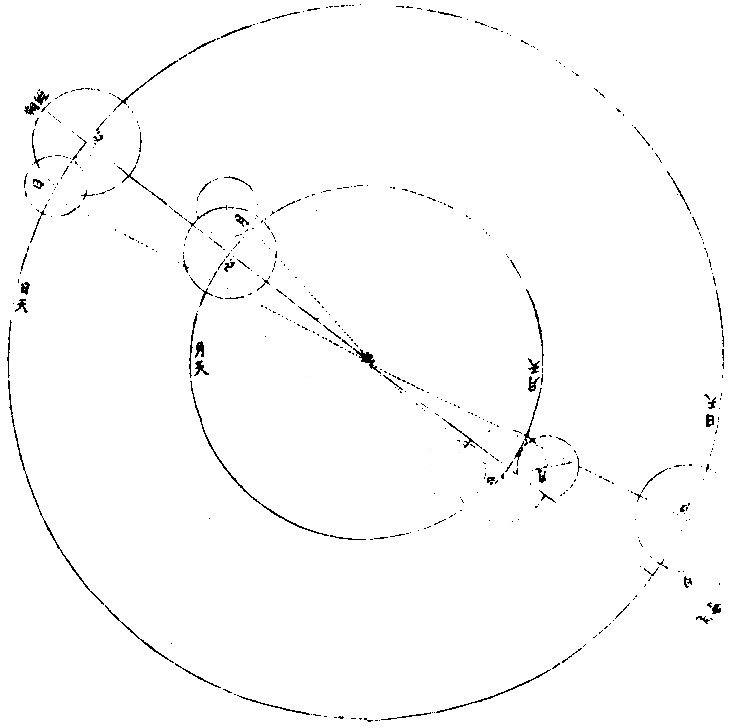 日月合朔图说 日月本天,俱包地外,而日远月近,二天悬殊。又有均轮小轮,高卑远近,遂与地心不符。自地心出线,上指日月本天,两均轮心相参,直为经朔。此止就本天之平度,而约其泛曾之日分也。自地心出线,上指日月两体,径中心相参,直为“合朔。”此用均轮、小轮上之加减,而定其实会之日分也。弦望加时,星曜同度,其理仿此。 月蚀诸象图 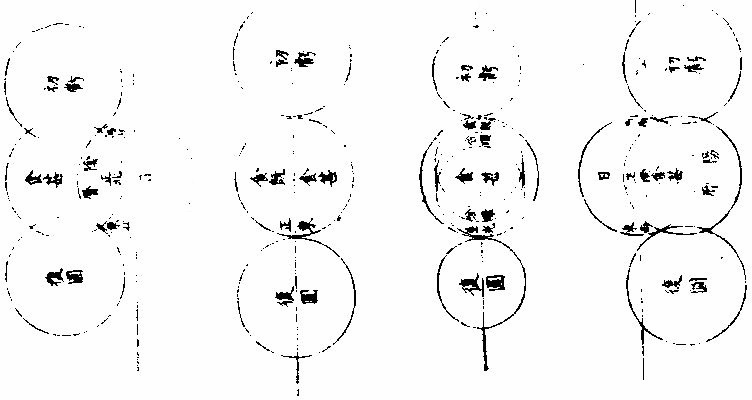 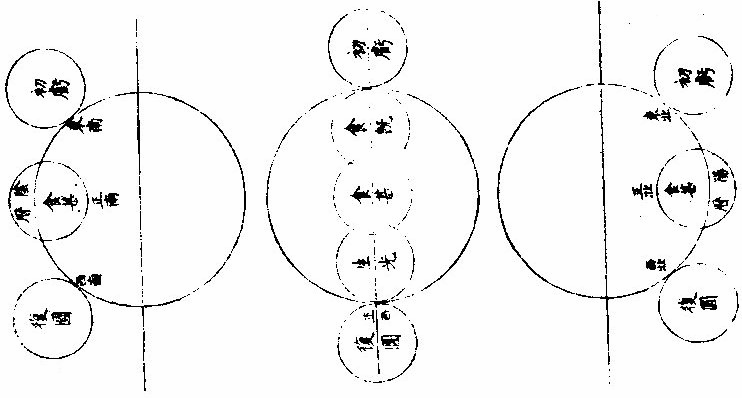 交蚀诸象图说 “日月之蚀,皆月之行度使然。日天高而在外,月天卑而在内,周绕大地,相距远近,时刻不同。合朔而月在日下,则月体掩日;定望而月与日冲,则地隔日光。故日蚀者,月本暗而来掩之也;月蚀者,月入景而不得借光也。月来掩则日为主,而人目所见者即得日光之亏复;月入景则景为主,而人目所见者反得月体之盈亏,此始终方位之所以异也。日为主而月来掩之,故亏起日体之西而复于东,在阳历则所食偏南,在阴历则所蚀偏北。景为主而月来就掩,故亏起月体之东而复于西,在阳历则所蚀偏北,在阴历则所蚀偏南。”又日月体径,约略相似,实则日大而月小。日蚀至既,每显金环,不既者分为三限:月东轮切日西轮,曰初亏,月中径齐日中径,曰蚀甚,月西轮切日东轮,曰复圆。蚀既者分为五限。初亏、蚀甚之间,两西轮齐,曰蚀既。蚀甚、复圆之间,两东轮齐曰生光。金环者分为七限,蚀既、蚀甚之间,环光自微至着,曰“合环。”蚀甚、生光之间,环晕全而复缺,曰分环。此日蚀之始终也。月径小于景径二倍半有奇。每蚀既之后,月行暗中,为时颇久。不蚀既者分为三限:月东轮切景西轮曰初亏,两中径齐曰蚀甚,月西轮切景东轮曰复圆。 蚀既者,分为五限:初亏、蚀甚之间,两西轮齐曰蚀既。 蚀甚、复圆之间,两东轮齐曰生光。此月蚀之始终也。 总之,月行甚速,经度纬度与日相交相距,是生薄蚀。 故日月之蚀,皆由月之行度使然也 日月地半径视差图 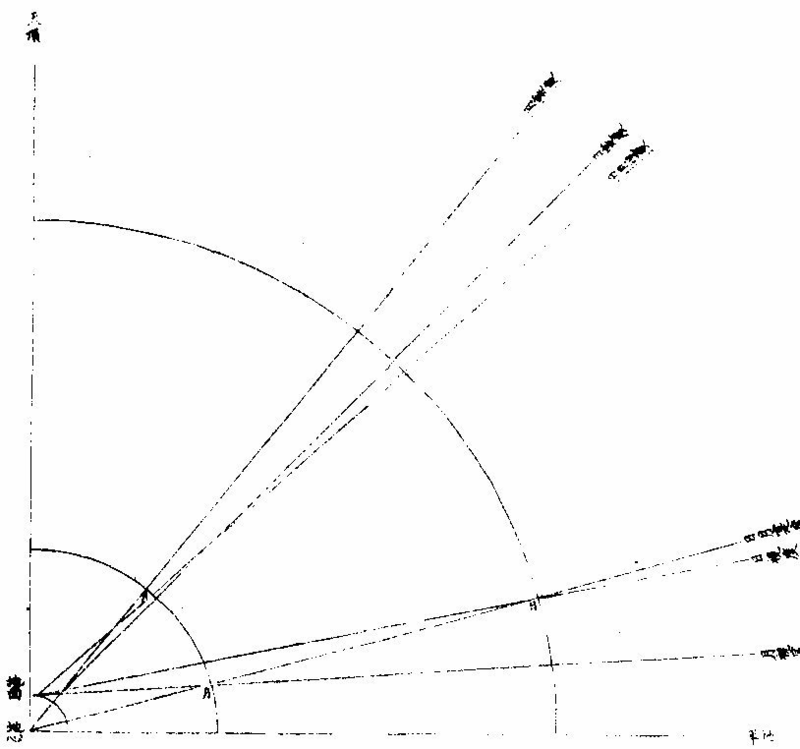 《日月地半径视差图说》。 “历法屡经修改而渐密,然测候之时,较推步之数,往往未尽合者。古人但知以天定度,未悟以地合天也。 地居天中,虽云微渺,然析其广轮,则周围数万里;计其直径,则中边亦万余里,人物环居其上,目力止凭地面所见,而天行枢轴在心,立法必以地心为准,故其差数一生于地势焉。有地心,有地面,相距为一半”径,于是从地心而推日月实度所在,又从地面而得日月视度所在,此一端也。一生于天体焉,有日天,有月天,远近各与地半径为比例,于是日天远,而实度与视度之差少,月天近,而视度与实度之差多,此二端也。又一生于地上之高度焉,有地平,有天顶,日月出地,渐升而高,于是近地平则实度与视度之差多,近天顶则视度与实度之差少。大抵渐高渐少,至天顶则无差,此三端也。 如下图地心出直线,指日月实度相合,及地面出直线,指日之视度在实度之下,又指月之视度亦在实度之下,而井在日视度之下。日天远而月天近,故差不同如此。上图地面出直线,指日月视度相合,及地心出直线,指日之实度在视度之上,又指月之实度亦在视度之上,而并在日视度之上。日天、月天,远近不同,故差不同如此。又上图高而近天顶,视差少,下图卑而近地平,视差尤多,此差恒降高为卑。测高度者,必于测高内加其时之差,而后得实高。推交会者,必于实会加减其时之差,而后得视会。此差为薄蚀凌犯之至要,而皆地半径之所生,亦曰《地半径视差》,亦曰高卑差。 |
| 虚阁网(Xuges.com) |
| 上一页 回目录 回首页 下一页 |